Log Pattern Recognition: LogMine
When retrieving logs from an application, you are often looking for outliers (such as a unique error) or what pattern occurs the most. However, defining patterns manually is time-consuming and requires rigour across projects. In this series of blog posts, we are going to explore automated Log Pattern Recognition.
Why
I recently began using Datadog Log Pattern and became addicted to it. Unfortunately, I was not able to find such a feature on Kibana or a query proxy able to do this analysis. If that does not exist, I might as well learn more about it and make one!
To my surprise, I did not find as many papers as I thought I would. And the number of papers with public implementations is even lower. Our series begins with a paper called LogMine: Fast Pattern Recognition for Log Analytics and an implementation made by Tony Dinh that helped me a lot to study LogMine’s behavior.
To my surprise, I searched for anything related to LogMine on Hacker News and only found Tony Dinh’s submission.
Defining the terms used in this article
Some terms used in this article can have several meanings. In Logmine’s context, the terms I use mean:
log: a log line (string)12:00:00 - My awesome logpattern: Expression extracted by the algorithm (array offield)[<date>, "-", "My", "awesome", "log"]field: Part of apattern/ Word from alog(Either a fixed value, a wildcard or avariable)cluster: represents a group of logs that were identified as close to each othersvariable: a user-provided regex used to identify a known formatnumber = \d+ time = \d{2}:\d{2}:\d{2}
An introduction to LogMine
The LogMine paper describes a method to parse logs, group them into clusters and extract patterns without any prior knowledge or supervision. LogMine can be implemented using MapReduce and works in a single pass over the dataset.
LogMine’s approach to grouping logs roughly works by:
- Parsing logs into patterns
- Grouping patterns into clusters if the distance between them is small
- Merging clusters into a single pattern
- Repeat from step 2 until you are satisfied
LogMine classifies fields into three categories:
Fixed value, a field that is constant across all logs in a cluster. This is detected at the pattern extraction step.Variable, a field that matches a pattern provided by the user. This is detected at the pre-processing step.Wildcard, a field that is not constant across all logs in a cluster. This is detected at the pattern extraction step.
Let’s illustrate how it works, step by step, using three simple logs:
10:00:00 - [DEBUG] - User 123 disconnected
10:30:00 - [DEBUG] - User 123 disconnected
11:11:11 - [ERROR] - An error occurred while disconnecting user 456
12:12:12 - [DEBUG] - User 789 disconnected
We will also define a variable <time> that follows the pattern
\d{2}:\d{2}:\d{2}.
Note
A good practice would be to define more variables to avoid forming two clusters
from logs with low similarity. For instance, we should define <number>
as \d+.
Depending on the pattern of your logs, defining a common field like <log-level>
as [(DEBUG|INFO|WARNING|ERROR)] might end up hiding information. This is
because a WARNING log with an error message might not be that important yet
the same log message with an ERROR level might have the exact information
you would like to highlight.
Log parsing and dense clusters identification
The first step is to parse logs into patterns and identify dense clusters. Dense clusters are clusters where raw logs are almost identical.
To do this, we begin by splitting logs into patterns (an array of field). The separator used by default is any whitespace character.
| 10:00:00 | - | [DEBUG] | - | User | 123 | disconnected | ||
| 10:30:00 | - | [DEBUG] | - | User | 123 | disconnected | ||
| 11:11:11 | - | [ERROR] | - | An | error | occurred | while | … |
| 12:12:12 | - | [DEBUG] | - | User | 789 | disconnected |
Next, we will tokenize the logs and identify variables (regex provided by the user).
<time> |
- | [DEBUG] | - | User | 123 | disconnected | ||
<time> |
- | [DEBUG] | - | User | 123 | disconnected | ||
<time> |
- | [ERROR] | - | An | error | occurred | while | … |
<time> |
- | [DEBUG] | - | User | 789 | disconnected |
I stopped at the word while for readability reasons, but there’s no limit to
the number of fields.
Identifying dense clusters
Once this transformation is done, we will reduce these patterns into dense clusters. Identifying dense clusters can be seen as a special use-case of the clustering algorithm: we identify clusters but we skip the pattern extraction step as these patterns are nearly identical.
As such, I’ll first introduce the clustering algorithm and the notion of distance between patterns.
Grouping patterns into clusters
The clustering algorithm takes a list of patterns and identifies patterns that are close to each other. Both the Tony Dinh’s implementation and the paper uses the distance defined as:
With P and Q, two patterns.
If the distance between the two patterns is inferior to a threshold MaxDist
defined internally, then the two patterns are considered a member of the same
cluster.
This comparison process can be optimized by skipping unnecessary work if the
sum is already greater than our MaxDist.
This is valid because the elements inside the sum can’t be negative.
The scoring function proposed in the paper allows for tweaking weights depending on the field type.
In order to keep performance, the scoring function can’t return a negative
value. Therefore k1 and k2 can’t be negative.
Note
The definition of this scoring function seems to have left some place for interpretation:
- Tony Dinh’s implementation checks for equality if both value are fixed values.
- LogPai’s LogParser dropped the concept of variables and uses k2 to tune wildcards weight
Let’s define k1=1 and k2=1, these are the weight used by Tony Dinh’s
implementation and recommended by the original paper.
Applying the clustering algorithm
For this example, I will use the original paper recommendation (MaxDist=0.01).
The MaxDist parameter is used to tune the algorithm sensitivity: the higher
MaxDist, the more patterns are detected.
If MaxDist is too high, patterns are grouped into very large clusters and
pattern extraction become meaningless.
| Fields from | Fields from | Score | Sum (Total) |
|---|---|---|---|
<time> |
<time> |
||
- |
- |
||
[DEBUG] |
[DEBUG] |
||
- |
- |
||
User |
User |
||
123 |
123 |
||
disconnected |
disconnected |
The two logs belong to the same cluster as .
| Fields from | Fields from | Score | Sum (Total) |
|---|---|---|---|
<time> |
<time> |
||
- |
- |
||
[DEBUG] |
[ERROR] |
0 | |
- |
- |
||
User |
An |
0 | |
123 |
error |
0 | |
disconnected |
occurred |
0 |
The two logs do not belong to the same cluster as .
Note
As we are using MaxDist=0.01, and since the logs in my example are very short,
we will only identify logs that are identical. For this reason, we can use the
clustering algorithm to identify dense clusters by skipping the pattern
recognition step.
Pattern detection
In sequential (as opposed to MapReduce) mode, each time a pattern is inserted in a cluster, LogMine will try to extract patterns from them. LogMine knows only how to identify two types:
- Fixed values
- Wildcards
While it seems rather strict, remember that the early pattern detection during tokenization already took care of identifying user-defined patterns.
Generating the pattern each time a new pattern is added allows LogMine to only keep one representative for each cluster. This is a very important factor to reduce memory usage.
MapReduce behavior is described later in this article.
As patterns in the same cluster can have a different number of fields, the paper uses the Smith-Waterman algorithm to align them. The Smith-Waterman is mainly used in Bioinformatics to align sequences. It is interesting to see an algorithm like this applied to log pattern recognition.
Once the two patterns are aligned, we compare one by one the field:
- If the value is equal, we assign a fixed value
- If the value is different, we assign a wildcard pattern
The Smith-Waterman algorithm adds placeholders to align logs. These placeholders are never equal to a field value. This means that aligned parts of a log are always identified as wildcards.
The output of the pattern detection algorithm is a new list of patterns.
Applying the pattern extraction algorithm
Let’s assume that the previous algorithm identified a cluster with two patterns:
<time> - [DEBUG] - User 123 disconnected
<time> - [DEBUG] - User 789 disconnected
To stay consistent with how they were presented earlier, we will call them and .
| Result | ||
|---|---|---|
<time> |
<time> |
<time> |
- |
- |
Fixed value |
[DEBUG] |
[DEBUG] |
Fixed value |
- |
- |
Fixed value |
User |
User |
Fixed value |
123 |
456 |
Wildcard |
disconnected |
disconnected |
Fixed value |
Result of applying the Smith-Waterman algorithm
Because examples in this article would have gotten very complex, I decided to not use non-aligned logs in my examples. However, you might be curious as to how the Smith-Waterman works.
On the implementation, LogMine would have aligned the two following patterns by
adding a None value in a field. For instance:
<time> - [DEBUG] - User 123 disconnected
<time> - [DEBUG] - User 123 has disconnected
would become:
<time> - [DEBUG] - User 123 <None> disconnected
<time> - [DEBUG] - User 123 has disconnected
The Smith-Waterman does not understand patterns. The Smith-Waterman uses the same scoring function as the clustering algorithm. As such, if two fields are not equal, there is no guarantee that the placeholder will be inserted properly.
If we tweak our previous example to:
<time> - [DEBUG] - User 123 disconnected
<time> - [DEBUG] - User 456 has disconnected
The Smith-Waterman algorithm would transform it to:
<time> - [DEBUG] - User <None> 123 disconnected
<time> - [DEBUG] - User 456 has disconnected
The alignment was added before the user identifier.
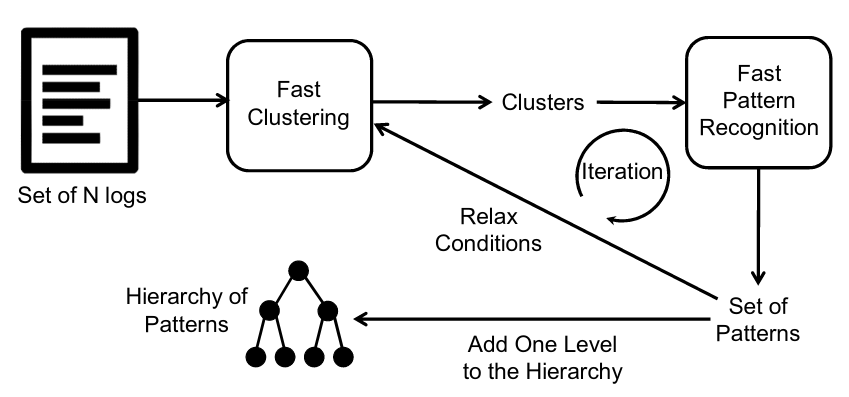
Repeat until satisfied
As the pattern extraction algorithm returns a list of patterns, we can relax
MaxDist and feed this list back into the clustering algorithm.
In 3.4 Hierarchy of Patterns, the paper describes a process to generate a
hierarchy of possible patterns from very strict to very lax. This process works
by repeating the clustering and extraction steps several times while multiplying
MaxDist by an factor.
Tony Dinh’s implementation does not relax MaxDist over several iterations and
prefers a single iteration. While very efficient, this reduces accuracy and
requires a better initial tuning.
“Simulating” the nth iteration
Let’s use the same four logs as previously defined. At this step, we will have three patterns as was merged with in a dense cluster.
Let’s also assume that MaxDist value is now 1.6.
Note
Skipping to MaxDist=0.6 (badly) simulates a high level in the hierarchy of patterns
which allows me to present an example where patterns are actually identified.
With an factor of 1.3, this would be somewhere between the 16th
iteration (MaxDist=0.51) and 17th iteration (MaxDist=0.66).
Let’s illustrate by applying the distance formula between our first log and the others.
| Fields from | Fields from | Score | Sum (Total) |
|---|---|---|---|
<time> |
<time> |
||
- |
- |
||
[DEBUG] |
[ERROR] |
0 | |
- |
- |
||
User |
An |
0 | |
123 |
error |
0 | |
disconnected |
occurred |
0 |
The two logs do not belong to the same cluster as .
| Fields from | Fields from | Score | Sum (Total) |
|---|---|---|---|
<time> |
<time> |
||
- |
- |
||
[DEBUG] |
[DEBUG] |
We stop early as the sum has already reached the threshold.
The two logs belong to the same cluster as . The sum can only grow and we can therefore stop the computation here.
We can group and inside the same cluster and in another. When scanning a new log, we will compare it to all clusters.
Returning relevant patterns
When implementing hierarchy of patterns, we obtain a tree (or an array of lists) where each level represents a different level of sensitivity. To find the right level to return, we need to define a way to rank each level.
The LogMine paper introduces a Cost function to determine the cost of a level.
This formula introduces three new tunable parameters:
- controls the weight given to wildcards ()
- controls the weight given to variables ()
- controls the weight given to fixed values ()
As the tree allows us to calculate a number of pattern (clusters) per level, we can allow the end user to provide a maximum number of pattern.
Scaling via MapReduce implementation
In the LogMine algorithm, each part cam be implemented using the MapReduce framework.
Note
When using the MapReduce framework, we split Log Clustering and Pattern Recognition into two distinct steps. This means that we need to store every log representatives of a cluster.
Scaling dense cluster identification
Implementing the identification algorithm using the MapReduce framework can be done easily:
- The map function maps logs to a key-value pair. The key is a fixed number and the value is a pattern.
- The reduce function merge these pairs together using the algorithm seen earlier. Remember that this step only keep one representative.
This step being only executed once and the number of cluster identified being low enough allows us to use a single key.
Note that the map function is only doing work when parsing logs. Once we are working with patterns, we can simply use the output from the pattern recognition in the clustering step.
Scaling pattern clustering
Just like dense cluster identification, pattern clustering does not require much work:
- The map function is a passthrough which creates pairs just like the previous algorithm.
- The reduce function merge these pairs and keep all representatives in the final pair.
Keeping all representatives allows the pattern recognition to work in a separate workload.
The output of this step is a list of all clusters identified.
Note that the reduce order can change clusters but this is not an issue over iterations because these clusters will be merged in the next iteration.
Scaling pattern recognition
Finally, the pattern recognition takes the input from the clustering algorithm:
- The map function maps a cluster to a list of pairs where the key is an identifier for the cluster and the value is a pattern.
- The reduce function merge these pairs by executing the pattern extraction algorithm.
The output of this function is a list of patterns.
Wrapping up
What I find really interesting about LogMine is the ability to change nearly every algorithm (such as the Scoring and Pattern Detections algorithms) without impacting the algorithm as a whole.
While all the algorithms in LogMine can be tuned, LogMine as a whole is not easy to tune:
MaxDistand create a trade-off between accuracy and performancek1andk2are hard to optimize- , and can be highly correlated with what variables the end user provided and on what the logs structure is
Moreover, LogMine does not support multi-fields tokens. A token spanning over several fields can easily create enough noise to split a single pattern in several clusters.
You can see an example of multi-fields token not being parsed properly in the
Apache Logs demo on Github. The date is
formatted as [Sun Dec 04 04:47:44 2005] and LogMine is only able to extract
the time. While you can easily parse the date as a whole, parsing each of its
field creates a lot of false positive (a regular expression matching 04 as the
<day> will also match any integer with two digits).
LogMine also does not keep track of the number of logs identified by a pattern, but this can easily be implemented without impact on performance.
Finally, LogMine does not have any knowledge about log structure. This means
that if your log format has fields that can change order, you need to normalize
this order first. LogMine seems perfect to analyze the message itself, for
instance what remains once every logfmt fields have been parsed and removed.
Going further
For my use-case, it seems that LogMine is enough as long as I can find an algorithm able to generate a regular expression from samples. This algorithm must work in one pass and on streamed data to avoid requiring more than one representative log to work.
What’s next
The second part of this series will focus on a paper called Drain: An Online Log Parsing Approach with Fixed Depth Tree.
Thanks
A big thanks to Tony Dinh for his implementation of LogMine and for the kindly answering the questions I had.
I’d also like to thank Marc Schmitt and Brice Dutheil for reviewing this article.
Series
- Part 1: LogMine
- Part 2: Drain